À quoi ressemble un événement rare ?
Des physiciens théoriciens ont résolu les équations très complexes décrivant le transport de matière par diffusion le long d’un canal unidimensionnel, appropriées pour décrire la survenue d’événements rares. Ces résultats, dont la portée théorique est significative, décrivent paradoxalement comment se passe, de la façon la plus probable, un événement improbable.
Un des apports majeurs à la physique de la fin du XIXème et du XXème siècle a été de faire rentrer les phénomènes aléatoires dans la description théorique de la matière. Tout d’abord, Boltzmann et Gibbs ont montré que la notion d’entropie, un concept macroscopique dont Clausius eut l’intuition au XIXème siècle, était intimement liée aux distributions de probabilités des différents états microscopiques d’un système à l’équilibre. Plus tard, avec les travaux d’Einstein et de Langevin sur le mouvement brownien, puis ceux d’Onsager sur les processus irréversibles, on a pu montrer que des lois générales existent encore dans la description des phénomènes faiblement hors équilibre, héritées des propriétés des fluctuations aléatoires de l’échelle microscopique. Les régimes très fortement hors équilibre, eux, ont longtemps été considérés comme impossibles à décrire par une théorie globale, car trop complexes et trop sensibles aux détails subtils de chaque système. Cependant, depuis une vingtaine d’années, les physiciens se sont intéressés à la description des états loin de l’équilibre (donc rares) à l’aide d’un concept probabiliste (les « fonctions de grande déviation ») permettant de rechercher une certaine universalité dans la description de ces états. En caractérisant les fluctuations des moyennes temporelles de grandeurs physiques sur un temps long mais fini, les fonctions de grande déviation sondent naturellement les processus dynamiques sur des grandes échelles de temps.
Dans une collaboration récente, des chercheurs de l’Institut de physique théorique (IPhT, CNRS / CEA) à Saclay et du Tokyo Institute of Technology ont considéré un modèle très étudié de diffusion unidimensionnelle, le « processus d’exclusion symétrique », où des particules sur des sites discrets sont susceptibles de se déplacer au hasard sur l’un des deux sites voisins de celui qu’elle occupe seulement si le site cible est inoccupé (deux particules ne pouvant se superposer, voir figure (a)). Ils ont réussi pour la première fois à résoudre exactement les équations complexes décrivant la fonction de grande déviation caractérisant la quantité de matière qui sur un temps long donné, transite à travers le système. Ce résultat constitue un progrès significatif vers une approche quantitative générale des processus hors d’équilibre, et la compréhension quantitative des événements rares et des fluctuations dynamiques qui en résultent. Ce travail est publié dans les Physical Review Letters.
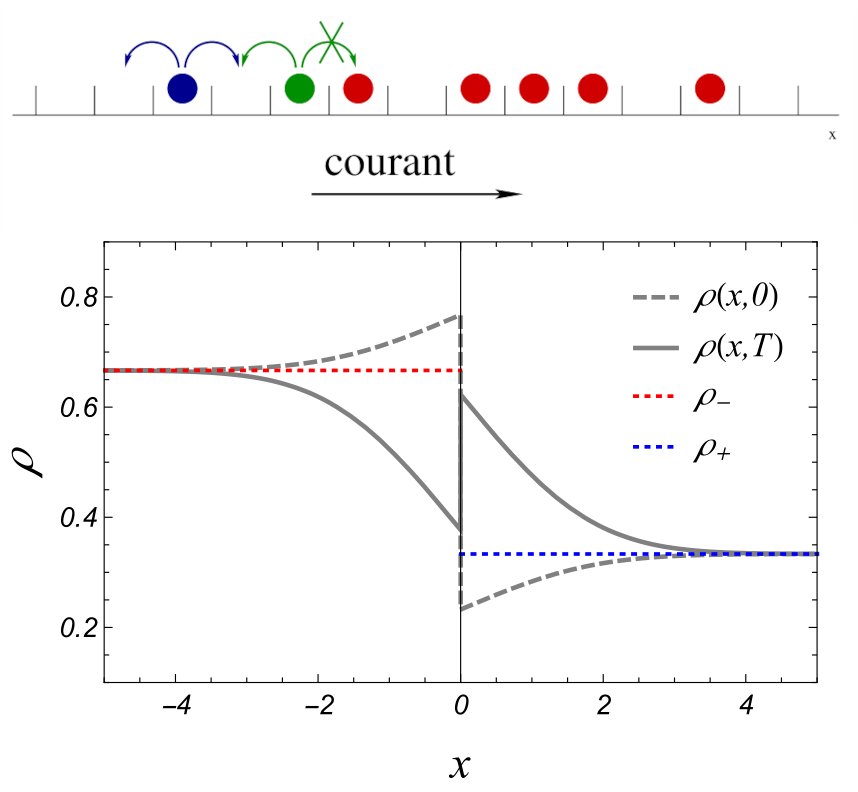
En bas : Évolution du profil de densité d’un fluide loin de l’équilibre qui produit un courant macroscopique donné. Afin d’optimiser le flux transmis, cette densité adopte une forme d’onde de choc qui s’inverse du temps initial t = 0 au temps final t = T. Les pointillés représentent les densités asymptotiques à l’infini ρ + et ρ −.
Crédits : IPhT (CNRS / CEA)
Références
Exact Solution of the Macroscopic Fluctuation Theory for the Symmetric Exclusion Process. K. Mallick, H. Moriya, T. Sasamoto, Physical Review Letters, publié le 19 juillet 2022.
DOI : 10.1103/PhysRevLett.129.040601
Archives ouvertes arXiv