Les réseaux complexes réinterprètent les quatuors de Beethoven
Une base de données recensant exhaustivement la succession des accords de tous les quatuors de Beethoven a permis leur analyse à la lumière d’outils développés pour la compréhension de l’architecture et l’exploration de grands réseaux contemporains, comme le Web, les écosystèmes, ou encore les interactions au sein de groupes sociaux.
La théorie des réseaux a permis de comprendre comment se structurent divers systèmes complexes tels que les interactions proies-prédateurs dans un écosystème ou l’organisation du Web. Elle a ainsi établi des lois universelles relatives aux propriétés statistiques de différents systèmes physiques, éclairant les mécanismes sous-jacents à leur formation et à leur dynamique. Cette approche a par exemple été appliquée avec succès aux réseaux linguistiques issus de textes ou de dictionnaires. Le corpus musical, qui a certaines similarités avec le langage, a fait l'objet de nombreuses études en lien avec la physique ou les mathématiques : traitement automatisé de l'analyse harmonique, analyse statistique, applications de l'intelligence artificielle... Mais il n'avait pas été jusque-là considéré du point de vue de la théorie des réseaux, alors que les différents éléments harmoniques d’une partition, se succédant selon une « grammaire » qui définit le style musical, ont une interaction de fait et ressortissent à une analyse de réseau. Alors que l'analyse statistique se borne à considérer les accords isolés (ou par paires ou triplets), cette approche permet donc de considérer le texte musical dans sa totalité et d'analyser les relations entre accords à une échelle plus globale.
Des physiciens du Laboratoire de physique théorique (LPT, CNRS / Université Toulouse – Paul Sabatier) et du Laboratoire de physique théorique et modèles statistiques (LPTMS, CNRS / Université Paris-Saclay) ont étudié la structure harmonique des quatuors de Beethoven par la théorie des réseaux. À partir d'une base de données d'analyse musicale des 14 quatuors établie par des musicologues, ils ont construit un réseau dirigé décrivant la dynamique harmonique au sein des phrases musicales successives. Les accords y sont considérés relativement à la tonalité locale, pour tenir compte de l’invariance globale de la musique par transposition (depuis la fin de la période baroque et l’établissement de la gamme dite « tempérée », toute pièce musicale peut en effet être translatée globalement en décalant toutes les notes d’un même intervalle sans altération perceptible du résultat). Par ailleurs, et de façon très naturelle, des connexions entre paires d’accords sont définies dans le réseau si une succession de tels accords existe dans une même phrase musicale, une pondération de ces relations rendant compte de la fréquence de ces associations. L'analyse des sous-structures de ce réseau révèle la présence de pôles d'attraction autour des degrés principaux de la gamme dans la musique occidentale (tonique, dominante, sous-dominante), avec des structures similaires d'une sous-structure à l'autre. De façon intéressante, l'existence de différentes périodes stylistiques dans l'écriture de Beethoven se manifeste de façon mesurable à travers des différences quantitatives dans les observables décrivant la topologie du réseau de relations entre accords.
Ce travail, qui ouvre la voie à des analyses similaires sur des bases de données récemment produites pour des compositeurs dont l'activité s'étend du 16e au 19e siècle, est publié dans The European Physical Journal B.
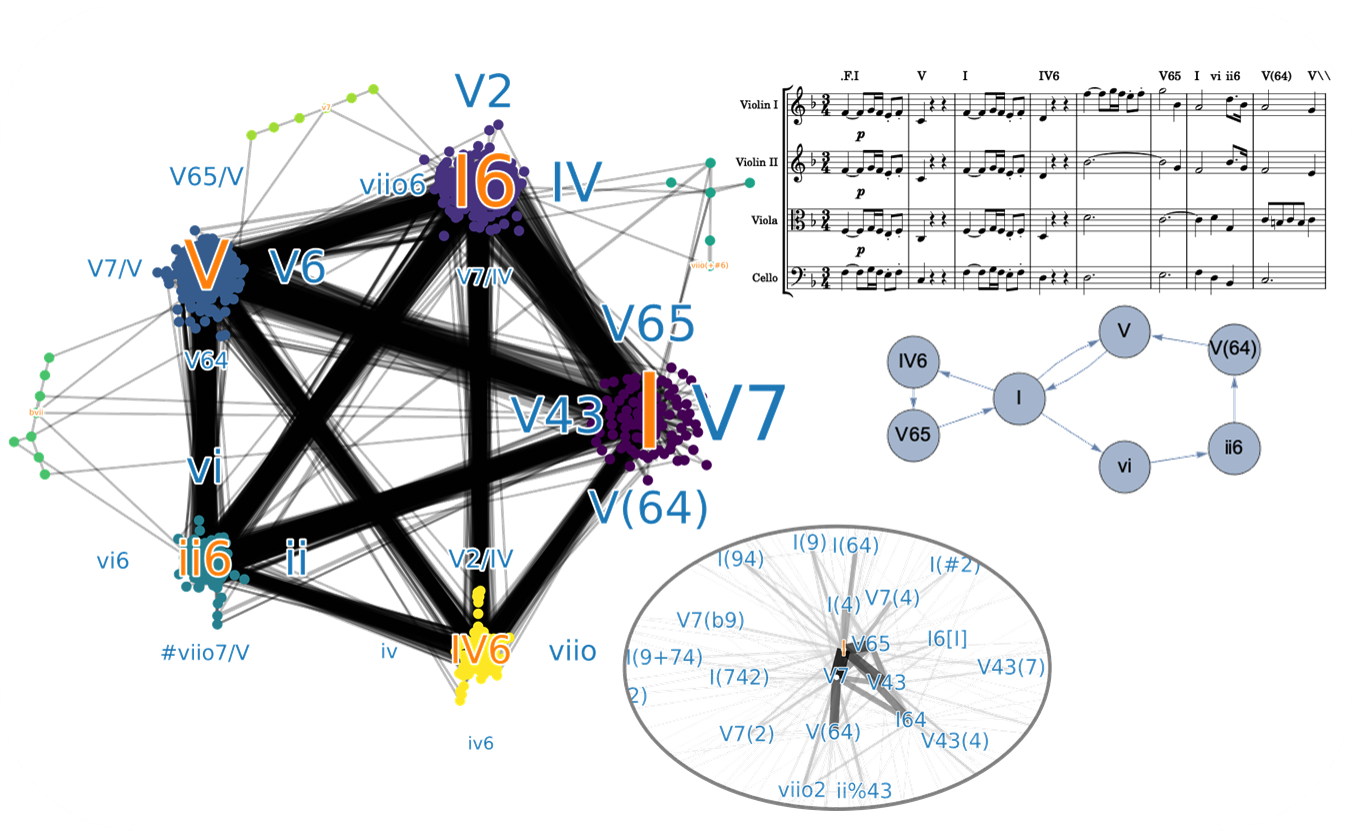
Début du premier quatuor à cordes de Beethoven et le graphe associé (à droite). Le graphe complet des accords du mode majeur (à gauche) se structure en pôles d'attraction autour des degrés principaux de la gamme. L'insert est un zoom autour du pôle d'attraction de la tonique (I).
Crédit : Olivier Giraud (LPTMS)
Référence
Harmonic structures of Beethoven quartets : a complex network approach. Th. Frottier, B. Georgeot, O. Giraud, The European Physical Journal B, paru le 02 juillet 2022.
DOI : 10.1140/epjb/s10051-022-00368-z
Archive ouverte arXiv