Dispersion of microorganisms: one law to rule them all

The Earth is populated by swimming microorganisms, such as bacteria, which are constantly moving. Their swimming strategies differ from one species to another, but because they involve reorienting themselves in randomly chosen directions, they are all “random walks.” Over long periods of time, this mode of movement is diffusive: bacteria initially released at the same location gradually disperse, much like tea infusing in still water. This spreading of the population, also known as dispersion, is quantitatively characterized by a parameter called the “diffusion coefficient.”

Approximately one-third of the 10³⁰ bacteria living on Earth today thrive in porous environments, i.e., environments consisting of interconnected cavities, which can be found in sediments, soils, rocks, food, and even inside the human body. Predicting the dispersion of bacteria in these environments is therefore a relevant issue in many contexts. Whether it is an infection of the human body or the contamination of food or aquifers, it is crucial to develop effective control strategies to know the diffusion coefficients associated with dissemination in these porous environments, as well as their dependence on the characteristics of each system. The difficulty, however, lies in the enormous diversity of situations encountered. Not only do bacteria exhibit many variations in their swimming strategies, but there are also a myriad of porous media, which differ in their structure, morphology, and characteristic sizes. Given the huge number of parameters that can vary from one system to another, how can dispersion be predicted? Is there a unifying principle that can simplify this problem?

The present research was conducted in the following CNRS laboratory:

• Institut lumière matière (ILM, CNRS / Université Claude Bernard Lyon 1)

The answer, surprisingly simple, has just been provided in a paper involving the iLM laboratory in Lyon and ETH Zurich. Researchers have shown that the dispersion of bacteria in porous media is universal: regardless of the porous structure or swimming strategy, dispersion follows a general law, which condenses the diversity of situations into a single mathematical relationship. To reach this conclusion, the first step was to numerically simulate bacteria moving in a porous medium. By rotating its flagella, a bacterium moves in a straight line for about a second before abruptly reorienting itself in another direction. This swimming strategy is called “run-and-tumble” and, depending on the species, there are many variations, particularly in the way the bacterium reorients itself. Furthermore, when the bacterium encounters the wall of the porous medium, it remains stuck there until it reorients itself and can move forward again in the liquid. 

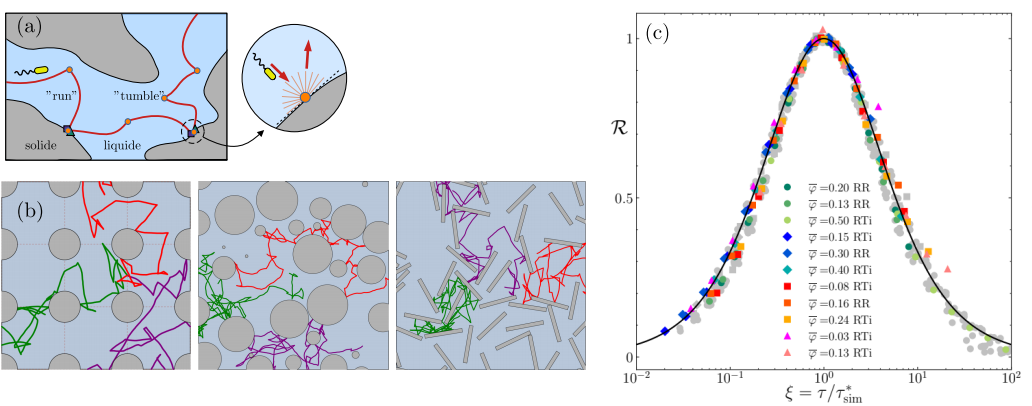
The researchers considered very different porous structures in their simulations: ordered or disordered, with circular or rectangular obstacles, low or high porosity, etc. In each case, the diffusion coefficient D was measured as a function of the average run time τ, i.e., the average time between two (random) events of bacterial reorientation. In all cases, the D(τ) curve shows a maximum. The surprising observation is that by simply scaling around the maximum, all of the curves, which cover dozens of different situations, can be superimposed on a single master curve, which defines a universal law of dispersion. 
What is the origin of this generic behavior? The answer was provided by an elementary model, in which the crucial quantity is the average time between two successive contacts with the wall. Counterintuitively, this average time does not depend on the movement strategy, but only on the average chord length of the structure. This geometric property, called Cauchy invariance, is what makes the dispersion law universal. 
Although inspired by the swimming behavior of bacteria, the dispersion law is actually relevant to a wide class of microorganisms, with potential applications in ecology. It remains to be understood how dispersion occurs when the movements of microorganisms are biased by an external factor, such as liquid flow or a chemical gradient. These results have just been published in Physical Review Letters.